What are string diagrams?

Many other people have done a much better job of explaining what string diagrams (and their underlying mathematics, a.k.a. symmetric monoidal categories) are than I can—see, for instance, [Selinger2010], or [Sobociński2015]—so here, I’ll just do the minimum required for the rest of this article.

The kinds of string diagrams I’m interested in are made up of boxes/morphisms that have some wires on their left and right sides. (A term described as “A/B” means “A” is the diagrammatic representation of the formal mathematical entity “B”.) The wires are labelled (in blue below) but sometimes you might not write the labels.

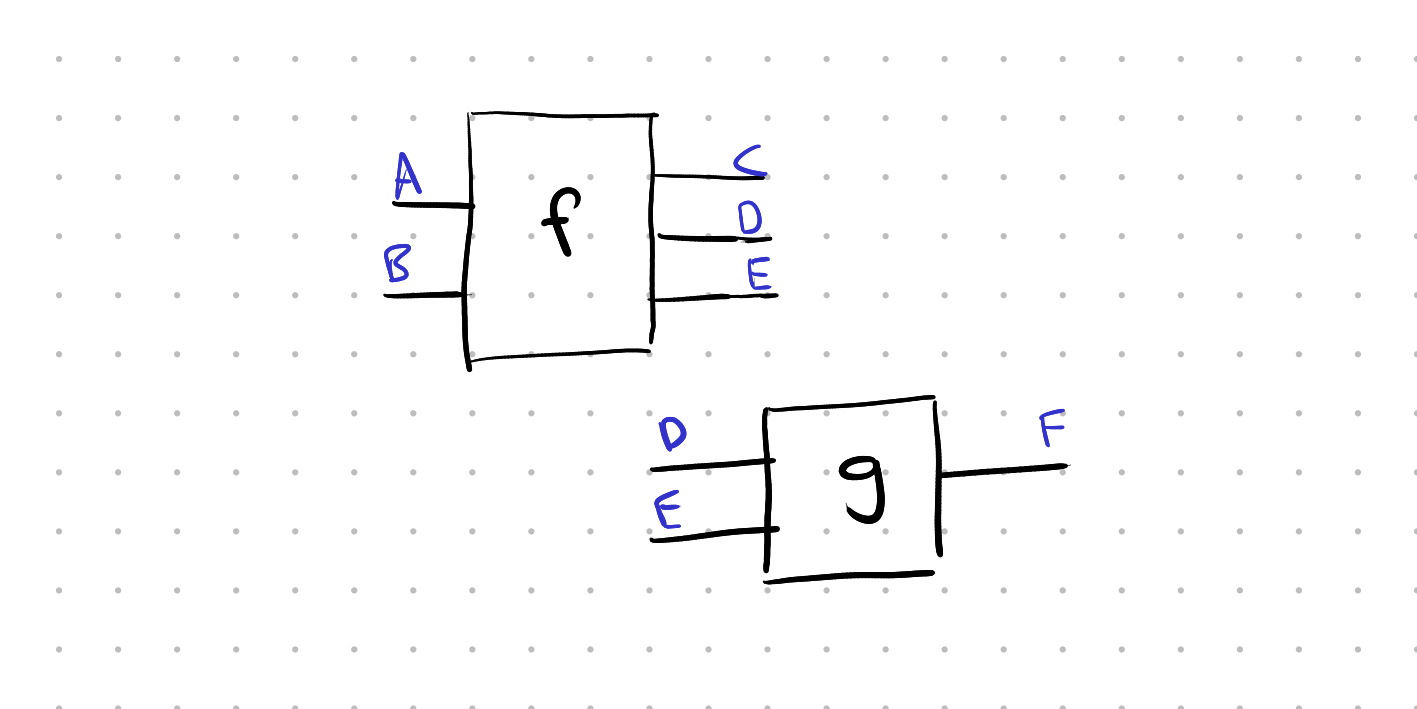
The source and target of a box are the labels of the wires on its left and right, respectively, but written with the stack/product operator ⊗ between them. Above, f has source A ⊗ B and target C ⊗ D ⊗ E, which we write as f: A ⊗ B → C ⊗ D ⊗ E.

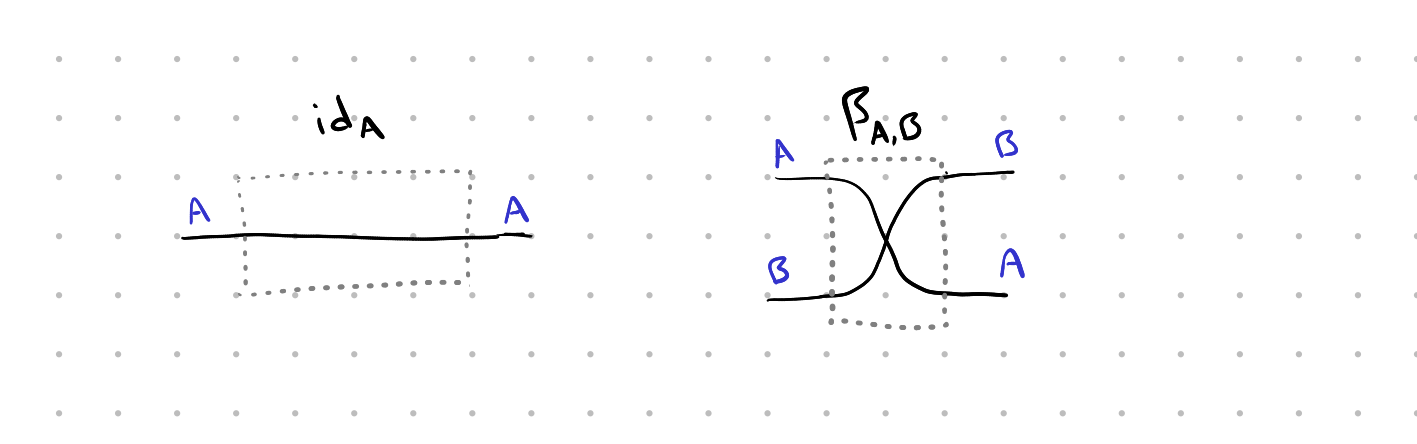
There are two kinds of primitive boxes: the identity box id_A: A → A for any label A, and the swap box β_A,B: A ⊗ B → B ⊗ A for any labels A, B.

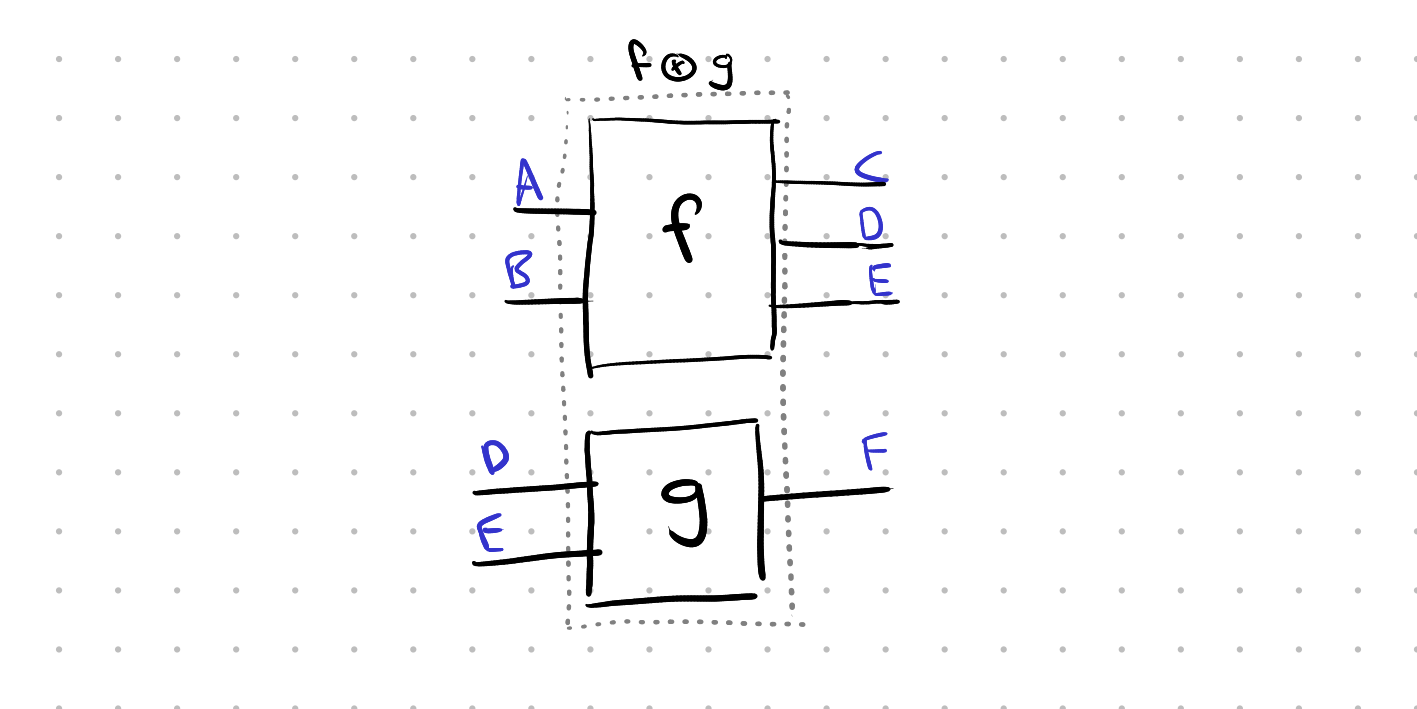
The stack operator has a second meaning: it also applies to boxes by stacking them vertically. So you can make f ⊗ g: A ⊗ B ⊗ D ⊗ E → C ⊗ D ⊗ E ⊗ F.

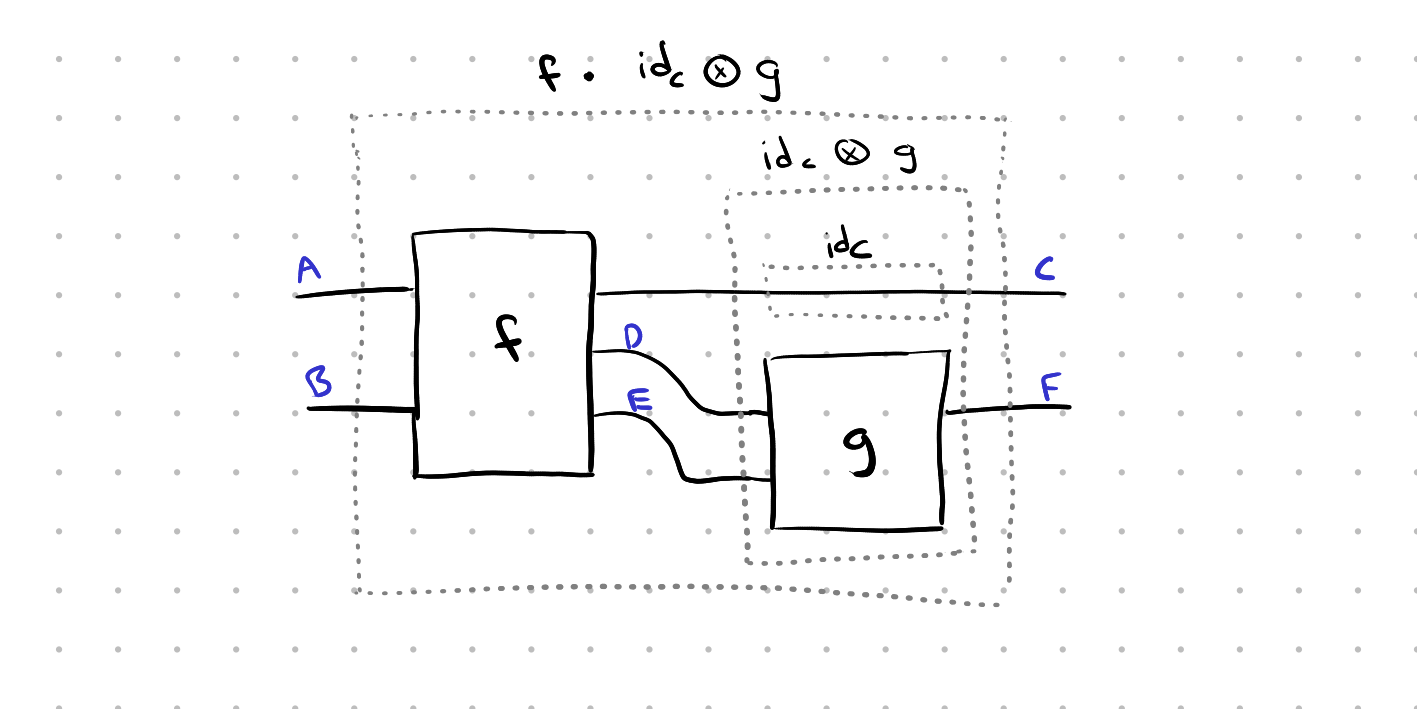
The last thing you can do with boxes is to connect/compose them by joining wires with the same label. This is denoted with ·, like f · id_C ⊗ g (note that ⊗ binds tighter than ·, just like multiplication binds tighter than addition in 2 + 3 × 5), which has source A ⊗ B and target C ⊗ F. The only restriction is that you can’t introduce loops.

So those are all the constructors of our diagrammatic calculus. A calculus also needs some axioms to make deductions about its terms. In our case, the axioms allow you to rewrite a diagram in any way that “graphically makes sense”, i.e. moving boxes around, swapping and unswapping wires, etc., while maintaining the connectivity of the diagram, i.e. what is connected to what. Two of these axioms, relating to swapping, bear special mention. They are called naturality and the hexagon axiom respectively:

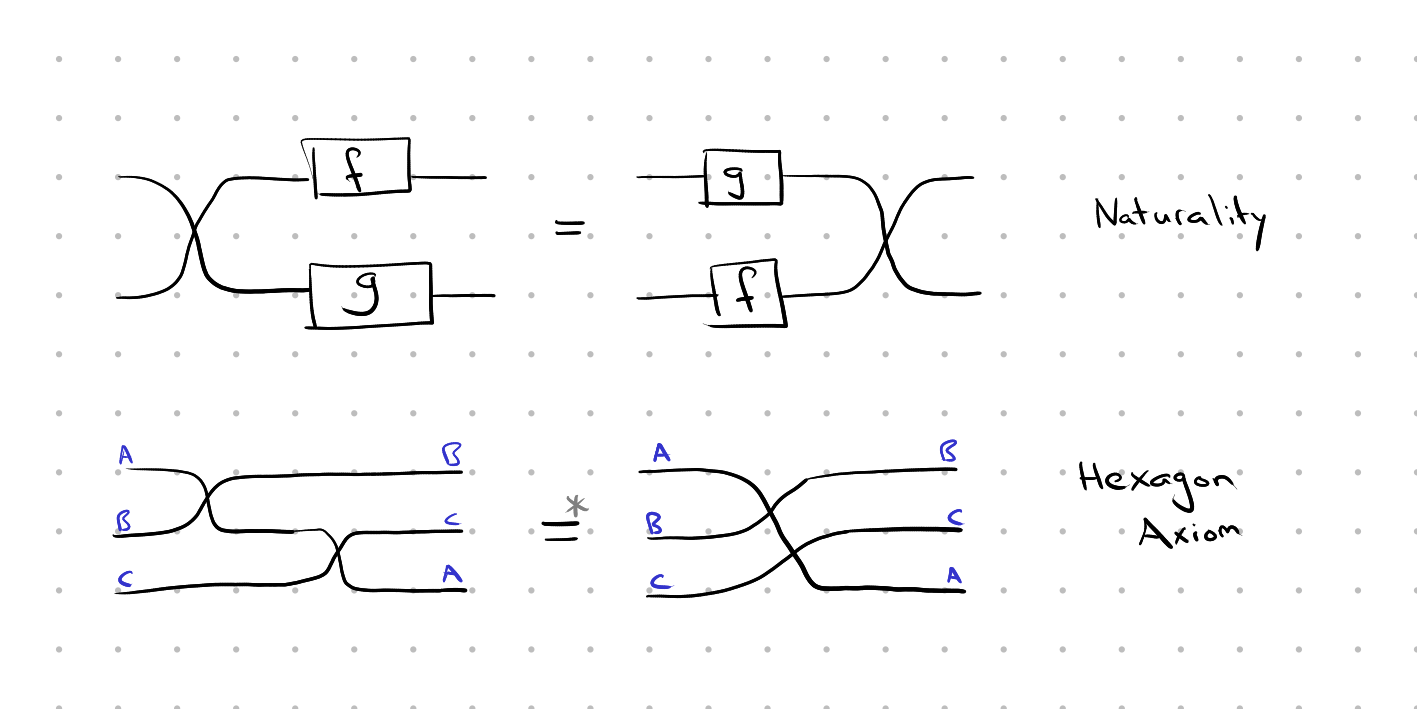
The hexagon axiom is a little tricky. It says that swapping A and B, and then swapping A and C, is the same as swapping A and the product B ⊗ C. But you, the astute reader, should be a little concerned at this point. We aren’t being fully precise, because we aren’t accounting for parenthesization/association: the left-hand side is (A ⊗ B) ⊗ C → B ⊗ (C ⊗ A) while the right-hand side is A ⊗ (B ⊗ C) → (B ⊗ C) ⊗ A. That brings us to…

What is SAADD and why do we want to factor it out?

SAADD stands for Symmetry, Associativity (of ⊗), Associativity (of ·), and Double Distributivity (of ⊗ and ·).

When we stack A ⊗ B ⊗ C or f ⊗ g ⊗ h diagrammatically, we don’t care how they’re associated; the stack looks the same either way. And we don’t bother indicating where or how the association changes in diagrams like the hexagon axiom. This is because, in the underlying mathematics, we have an isomorphism α_A,B,C between (A ⊗ B) ⊗ C and A ⊗ (B ⊗ C). For connections with ·, the property is even stronger, because · is defined to be such that (f · g) · h is equal to f · (g · h) for all morphisms. These are the two associativity properties.

Further, stacking and connecting distribute over each other. This is easiest to illustrate with a picture. (“Double distributivity” is probably not the right word, because it’s not like the distributivity of arithmetic × over +, where a × (b + c) = a × b + a × c, and a + b × c is irreducible. The right word is something like “bifunctoriality” but I don’t know enough category theory to say for sure. SAADD makes a nice acronym for the time being.)

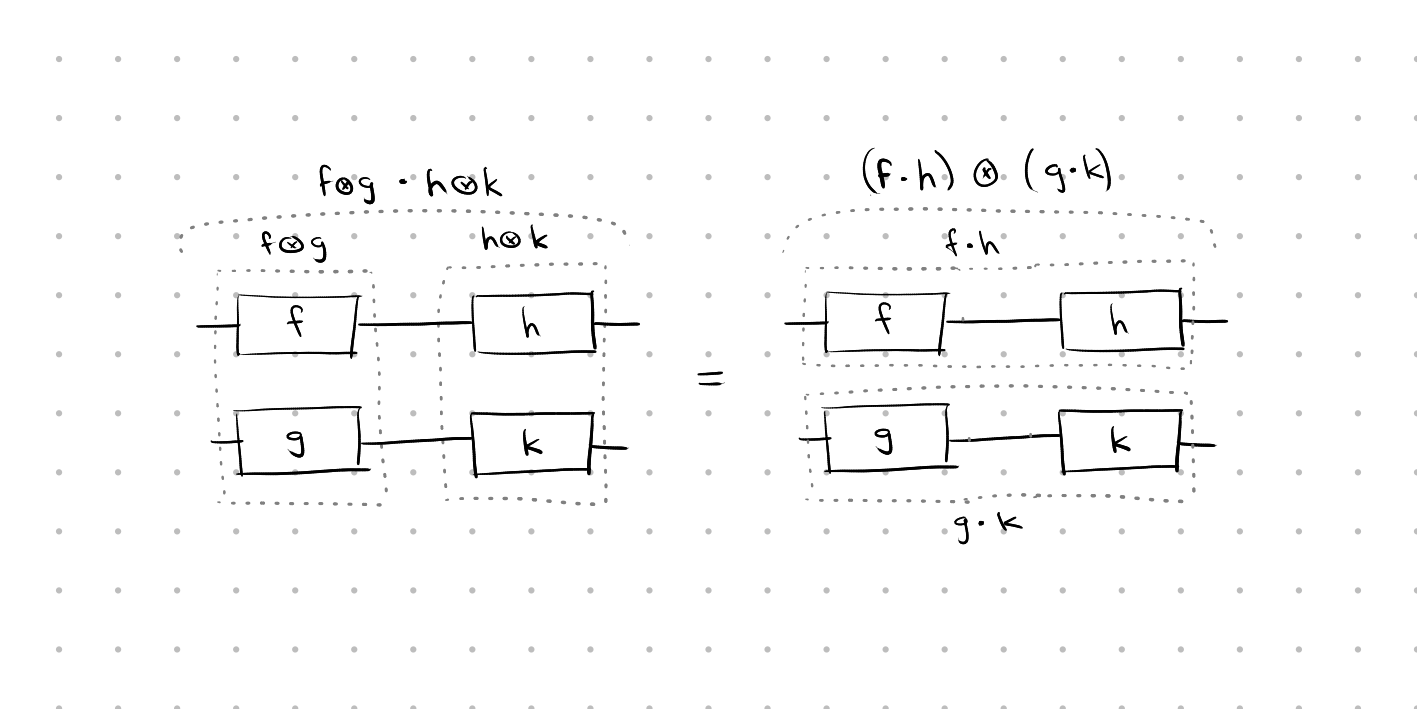
(corporate needs you to find the differences between this diagram and this diagram) – (they’re the same diagram)

Lastly, symmetry means that there is a self-inverse isomorphism between A ⊗ B and B ⊗ A, illustrated with a swap in our diagrammatic notation. Which means, for instance, that if you have g: A → C and f: B → D, stacked as g ⊗ f; and you know that f ⊗ g = h; then you can rewrite with that known equation as follows:

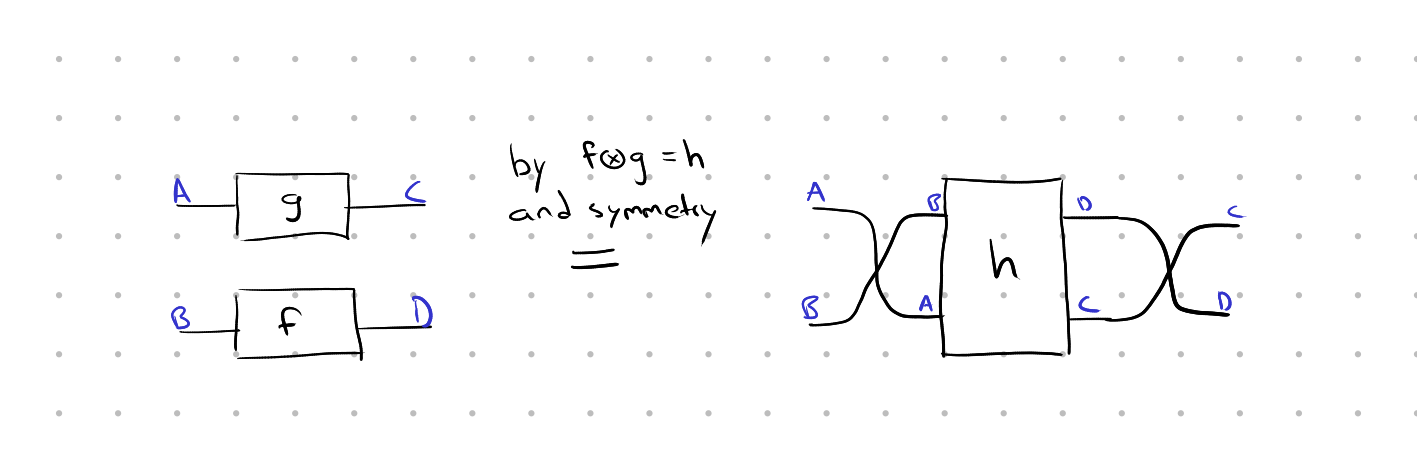
The point is, none of these SAADD properties matter when you’re doing diagrammatic rewriting, because they are obvious equalities or isomorphisms in the world of diagrams. You would not think of them as separate steps of your proof and you would not want to have to write them down. And in math papers, you don’t. But this is Interactive Theorem Proving, after all, where things are different…

Challenges with associativity

Let’s take a case study: the Yang-Baxter equation. It states

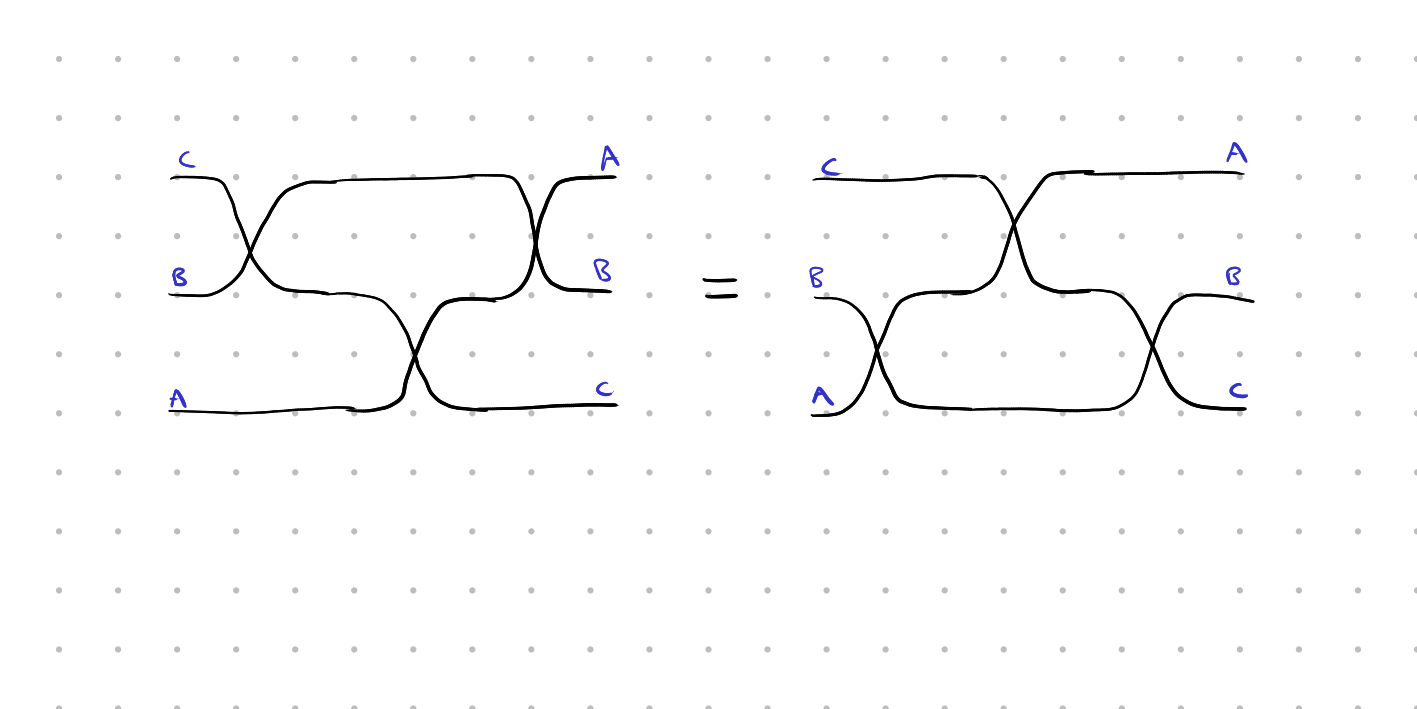
A diagrammatic proof

Proof by rewriting the left-hand side to the right-side side with axioms.

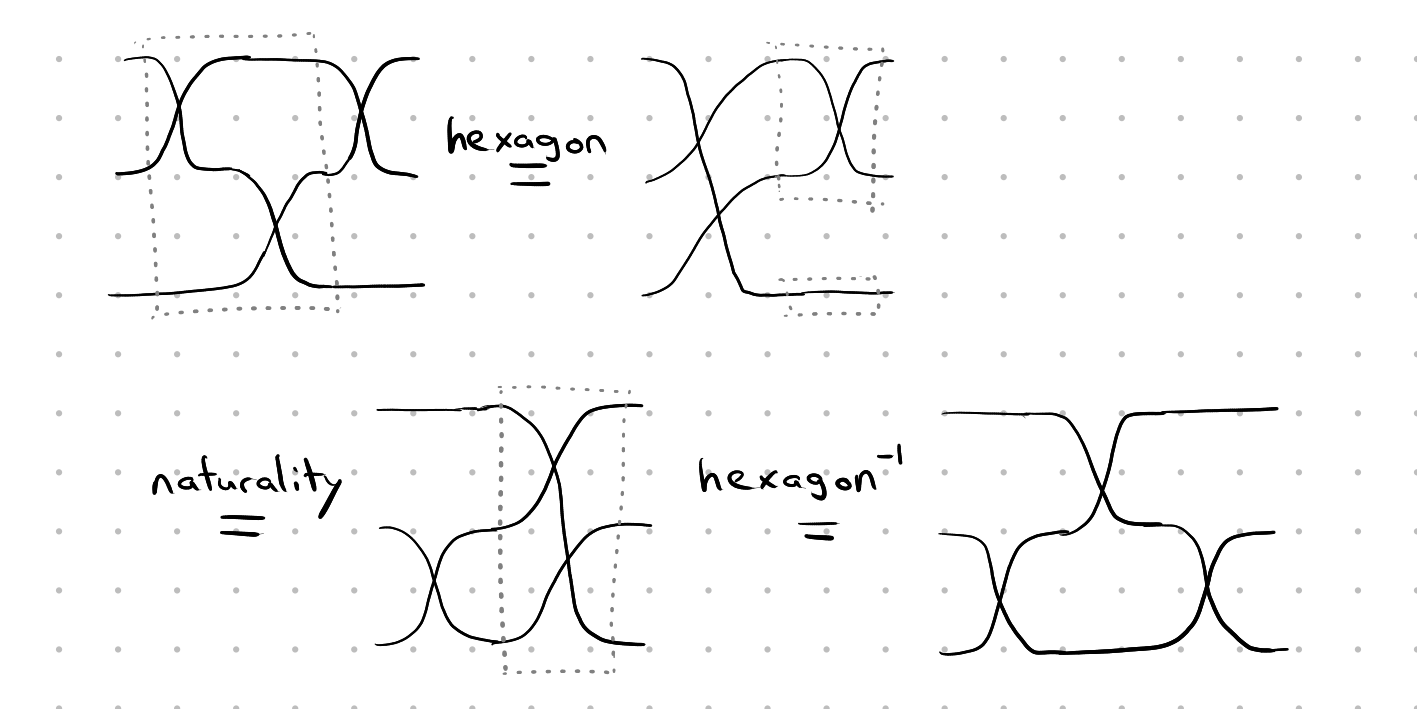
Easy.

A formal proof

Let’s write the left-hand side in mathematical terms. It looks like it’s the composition of three pieces:

• L₁:= β_C,B ⊗ id_A of type (C ⊗ B) ⊗ A → (B ⊗ C) ⊗ A

• L₂:= id_B ⊗ β_C,A of type B ⊗ (C ⊗ A) → B ⊗ (A ⊗ C)

• L₃:= β_B,A ⊗ id_C of type (B ⊗ A) ⊗ C → (A ⊗ B) ⊗ C

Hmm, the source and target types don’t quite match up. We need to interpose reassociation isomorphisms α_B,C,A: (B ⊗ C) ⊗ A → B ⊗ (C ⊗ A) between the first two and α_B,A,C^-1: B ⊗ (A ⊗ C) → (B ⊗ A) ⊗ C between the second two. So we get

(((β_C,B ⊗ id_A · α_B,C,A) · id_B ⊗ β_C,A) · α_B,A,C^-1) · β_B,A ⊗ id_C

The first step in the diagrammatic proof was to apply the hexagon axiom. Actually, why is it called that? The answer becomes clear when it is stated formally:

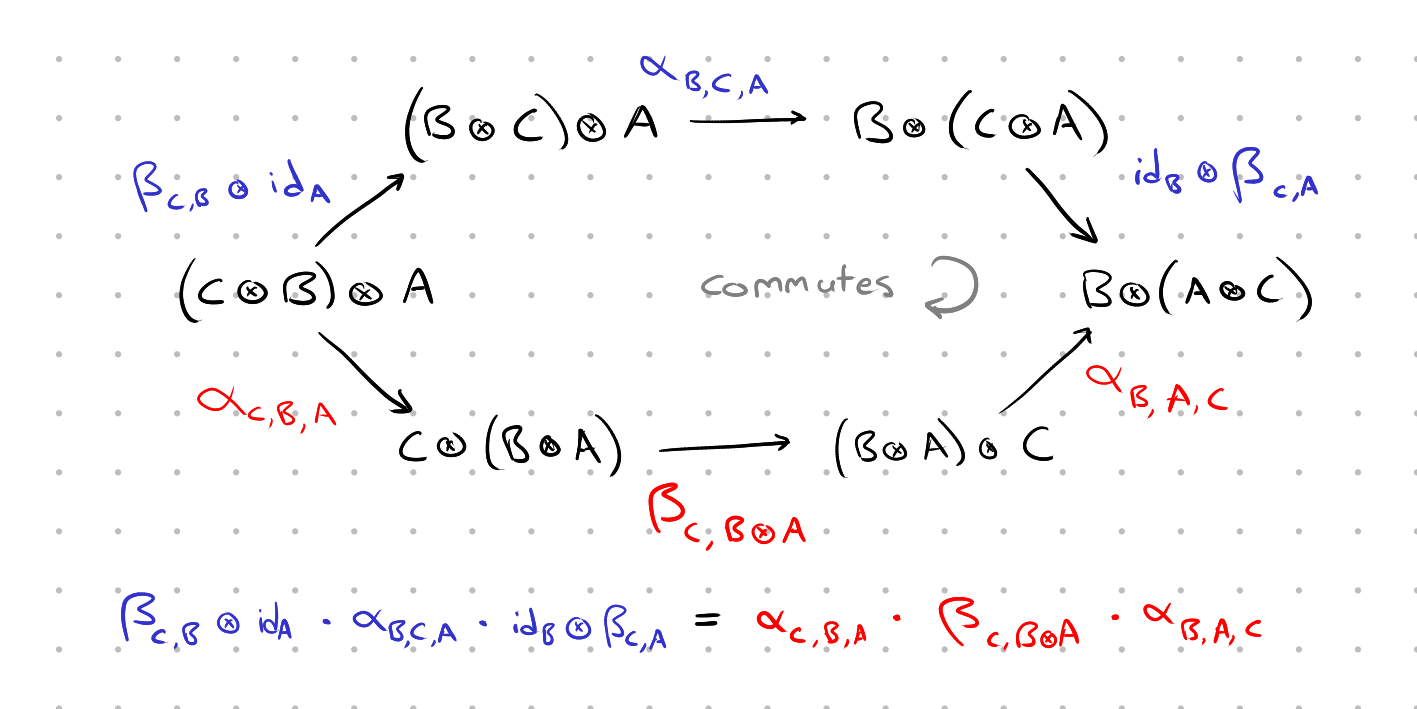
The whole diagram commutes, which means that any two paths between the same two objects are equal, i.e. the composition of the three morphisms on top equals the composition of the three on the bottom.

We can spot the left-hand side of the hexagon axiom in the left-hand side we wrote down previously. Let’s rewrite it with the right-hand side of the hexagon axiom.

(((α_B,C,A · β_C,B⊗A) · α_B,A,C) · α_B,A,C^-1) · β_B,A ⊗ id_C

And we can reassociate and simplify:

= ((α_B,C,A · β_C,B⊗A) · (α_B,A,C · α_B,A,C^-1)) · β_B,A ⊗ id_C

= ((α_B,C,A · β_C,B⊗A) · id_B⊗A⊗C) · β_B,A ⊗ id_C

= (α_B,C,A · β_C,B⊗A) · β_B,A ⊗ id_C

= α_B,C,A · (β_C,B⊗A · β_B,A ⊗ id_C)

Apply the naturality of swapping:

= α_B,C,A · (id_C ⊗ β_B,A · β_C,B⊗A)

Now we want to reverse rewrite the right-hand side of the hexagon axiom with the left-hand side, but we only have one of the terms, β_C,B⊗A. We’d need to compose it on both sides with the identity, then split the identity into the correct association isomorphisms and their inverses, then reassociate to isolate exactly the bottom side of the hexagon axiom, then rewrite, then… you get the idea. I’m not going to write this proof out in full because it’s tedious and not particularly illuminating. We have to worry ourselves with things like cancelling associativity operators which is far from the elegance of the diagrammatic proof we’re trying to emulate.

Challenges with symmetry and distributivity

In case you aren’t convinced yet, symmetry and distributivity properties pose exactly the same sort of problem in a formal setting—you don’t want to have to think about them but they keep popping up. Take, for instance, a simple monoidal law, where for all f: A → B and g: C → D,

f ⊗ id_C · id_B ⊗ g = id_A ⊗ g · f ⊗ id_D

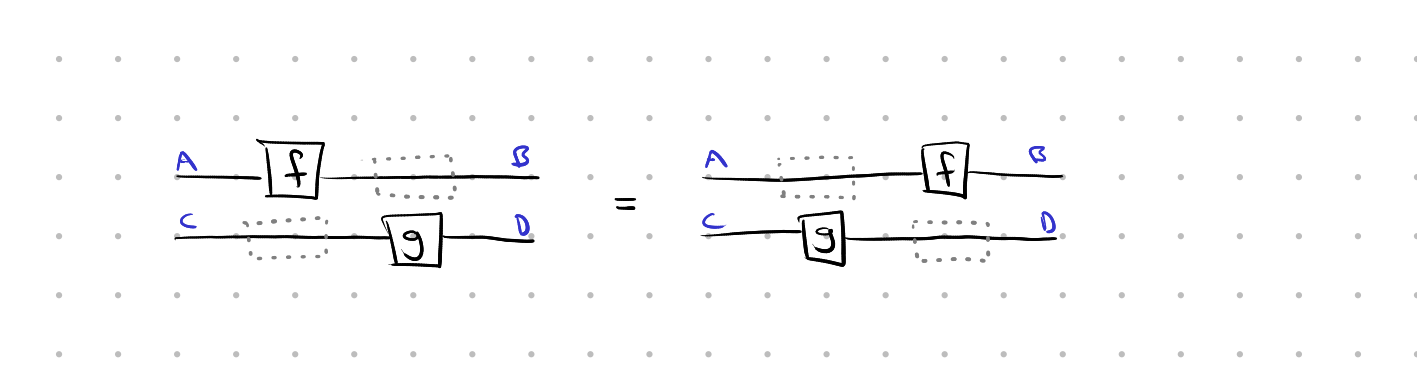
Diagrammatically, this seems obvious and trivial. But formally, the equalities we want to rewrite with are of the form id · f = f = f · id, and those terms don’t appear in the formula we wrote above. We first have to redistribute the composition over the product:

= (f · id_B) ⊗ (id_C · g) = (id_A · f) ⊗ (g · id_D)

Then apply the id properties, and finally redistribute the other way to get the formula we want. Ideally, we’d be able to rewrite f · id = id · f directly, or taking it even further, since this is a pretty basic identity, we’d be able to dispatch the whole goal with a single tactic.

Towards possible solutions

My first step was to set up the theory above in Coq exactly as described in [Selinger2010]. The style of formalization was inspired by ViCAR [ShahEtAl2024]. I started by formalizing a category as a typeclass with the basic constructors (like composition), together with a category coherence typeclass with the requisite properties (like associativity of composition). I extended those to monoidal categories by adding products and then to symmetric monoidal categories by adding swaps. (Remember that string diagrams represent morphisms in symmetric monoidal categories.)

Second, I registered morphism equality as an instance of an equivalence (with reflexivity, symmetry, and transitivity) as understood by Coq’s “generalized rewriting” mechanism, also known as setoid_rewrite. This lets you use the rewrite and setoid_rewrite tactics to rewrite equations with your own equivalences beyond Coq’s built-in syntactic equality =. I also had to register composition and products as operations compatible with morphism equality. This means we can “rewrite under” them, so to speak; or in other words, allowing us, for instance, to rewrite a = z in the term a ⊗ b · c, even though a is nested inside compositions and products.

Then, I decided to do the two proofs from before (the Yang-Baxter equation and the monoidal law) in full detail, without automation, just to confirm that they were possible, and to see just how tedious they got. Results: 26 Coq tactic steps for the first, 4 for the second. Here’s an excerpt from the first:

rewrite <- compose_associativity.
apply compose_compatibility; try reflexivity.
rewrite compose_associativity.
rewrite <- (compose_associativity (MC.(product_associativity) b c a).(b2a) _ _).
rewrite (product_associativity b c a).(inverse_a).
rewrite <- compose_associativity.

rewrite right_identity.

rewrite 4 compose_associativity.
rewrite <- compose_associativity with (f:=((identity _) ~⊗~ (SMC.(symmetry) a b).(a2b))).
rewrite <- compose_associativity with
  (f:=((identity _) ~⊗~ (SMC.(symmetry) a b).(a2b) ·
    (MC.(product_associativity) c a b).(a2b))).
rewrite <- compose_associativity with (h:=((identity _) ~⊗~ (SMC.(symmetry) b c).(a2b))).

rewrite symmetry_hexagon.

Lemma embedded_inverse_a: forall a b c L (l: _ ~-> L),
  (l · (product_associativity a b c))
    · (product_associativity a b c).(inverse_a) ≃ l.
Proof. (* by the inverse_a axiom *) Qed.

Proof.
  intros.
  do 2 rewrite_hexagon.
  repeat cancel_assocs.
  rewrite symmetry_natural.
  reflexivity.
Qed.

Proof.
  intros.
  rewrite <- 2 morphism_product_bifunctor_compose. (* redistributes terms *)
  rewrite ?left_identity, ?right_identity.
  reflexivity.
Qed.

ViCAR

ViCAR [ShahEtAl2024], or Visualizing Categories with Automated Rewriting in Coq, is recent in-progress work on exactly this problem of making string diagram rewriting more convenient in Coq, with a different approach. Instead of saying that SAADD properties should be completely transparent to the proof writer, ViCAR tries to provide (i) visualizations of string diagrams that show the inductive structure of nested compositions and products, integrated into the proof assistant via coq-lsp [CoqLSP2023]; (ii) high-level tactics that try to massage the goal into an equivalent form such that a given rewrite rule is applicable; and (iii) other high-level tactics that deal with simplification, such as cancelling out adjacent inverse morphisms and identity morphisms. Here’s an example of a ViCAR visualization (taken from their paper):

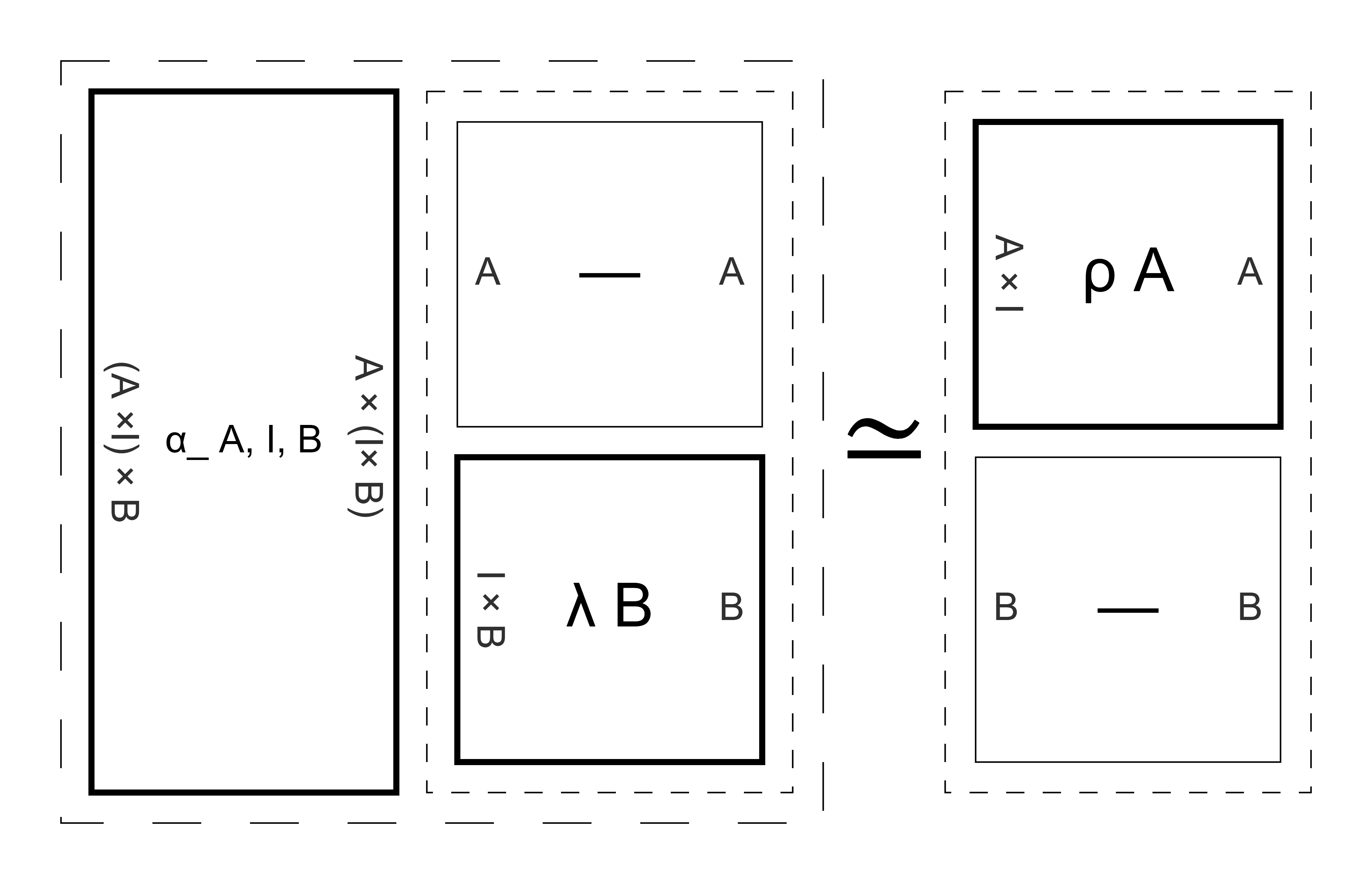
I tried doing the Yang-Baxter proof in ViCAR and it was pretty nifty!

Proof.
  intros.
  do 2 partners_rw hexagon_1.
  cat_cleanup.
  rewrite braiding_natural.
  reflexivity.
Qed.

And the monoidal law proof:

Proof.
  intros.
  rewrite <- 2 tensor_compose. (* redistributes terms *)
  cat_easy.
Qed.

Although I was also able to achieve similar proof length and convenience with much simpler automation, I think that’s just because my examples are quite simple, and to really evaluate ViCAR, I would need to try my hand at more complicated category theory proofs.

Something ViCAR does not currently aim to automate away is redistribution, as evidenced by the explicit second proof step in the monoidal law proof. This seems to be difficult to build into the current tactic-based approach. So the authors are working on an alternative with e-graph equality saturation to explore a graph of terms that are equivalent under rewriting, find a path that rearranges the term into an appropriate shape to apply a rule, and exports the proof back to Coq [ShahLehmann2024].

Chyp

Chyp [Chyp2023] is a graphical interactive theorem prover for string diagrams based on an alternative category-theoretical internal representation [BonchiEtAl2022] that enables “a convenient rewrite theory for string diagrams that automatically handles the extra ‘bureaucracy’ that comes from working with sequential and parallel composition together.” Sounds like exactly the problem we’re exploring. Let’s try it out:

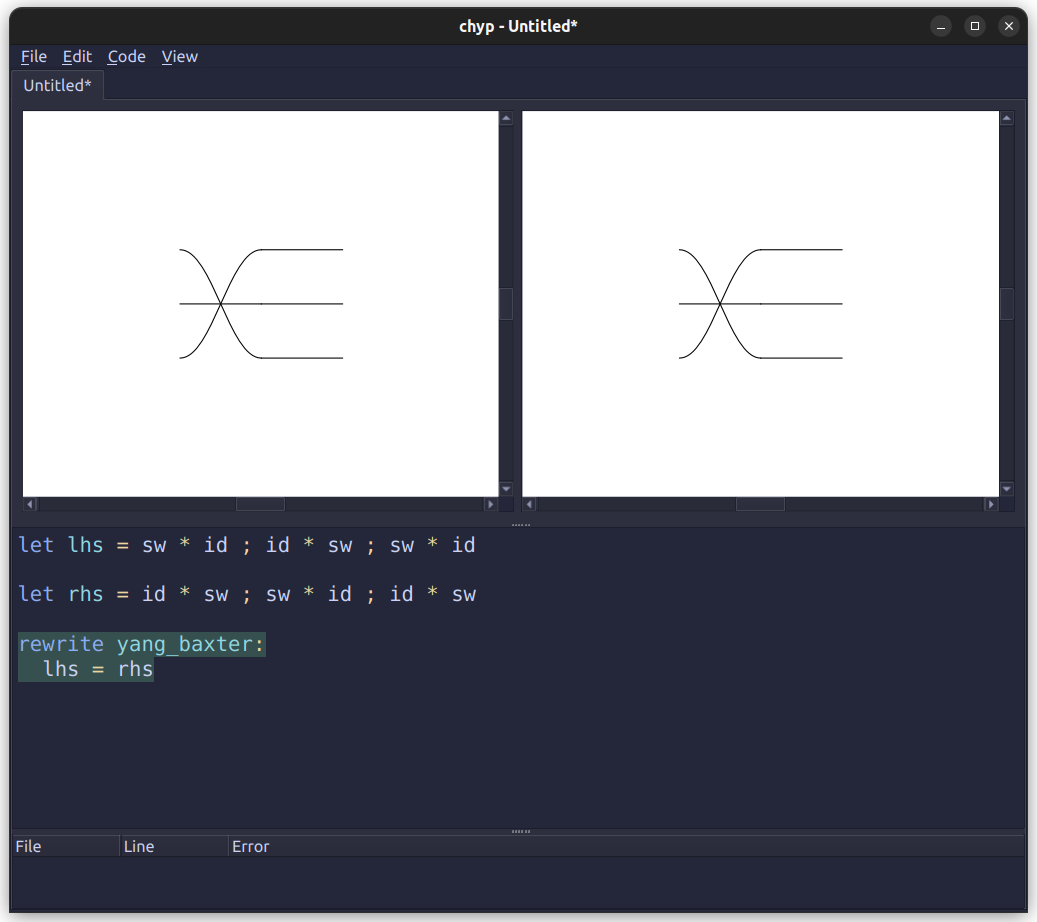
The first notable thing is that the left- and right-hand sides of the equation are displayed the same! In Chyp’s internal representation, they really appear to be the same diagram. The “proof” that they’re equal (we know it succeeded, because the rewrite rule is highlighted in green) is trivial. In Chyp, each step in a derivation needs a justifying by clause; if omitted, as here, the default is by reflexivity. Indeed, Chyp’s whole premise is that

“only connectivity matters. So, if two terms give the same diagram, like a * b ; c * d and (a ; c) * (b ; d), Chyp treats them as identical. Since under the hood, Chyp does everything with graph rewriting and not term rewriting, the prover handles all of this extra book-keeping for you.”

I couldn’t get it to produce a diagram with three separate swaps like my drawings above. At best, with two swaps, it produces

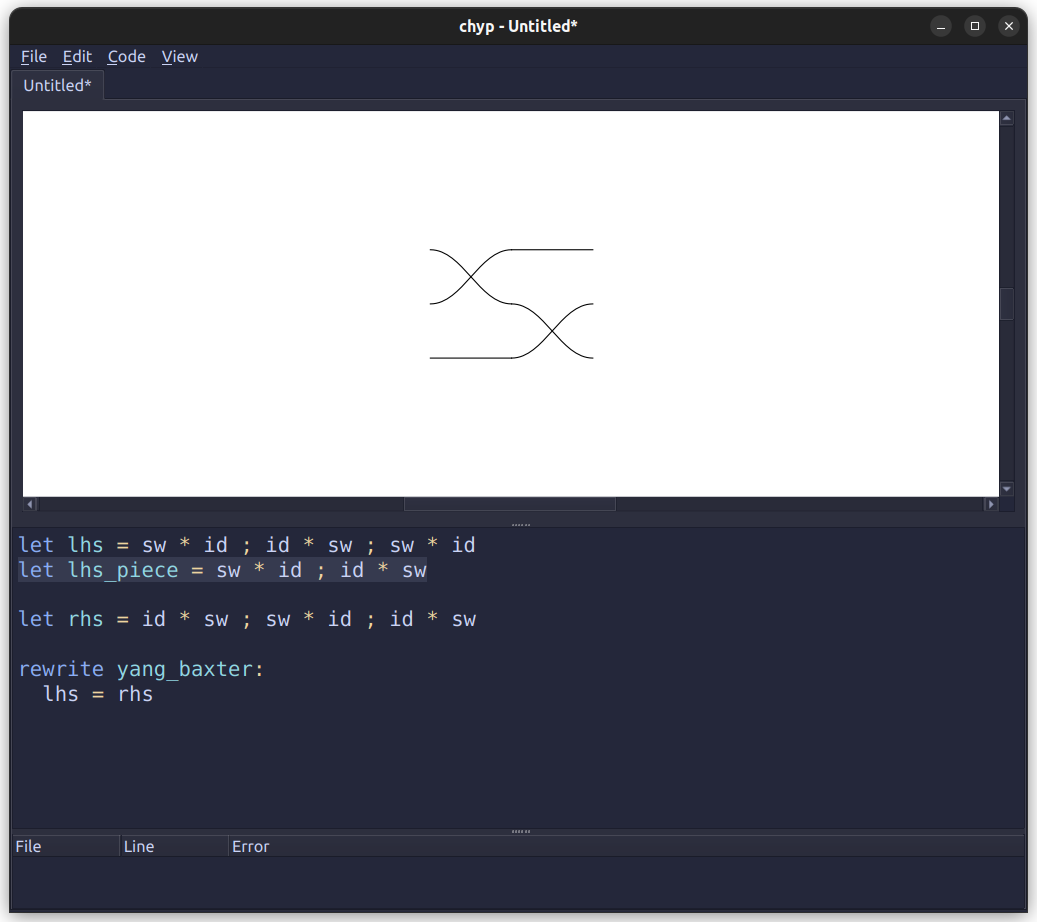
Which makes me question whether we ideally even want the three separate swaps in the first place, or Chyp’s “3-spider” representation is the correct one…

Chyp seems really powerful given how trivial our first example seems. I don’t have even the most basic grasp of the graph rewriting theory it is based on, so I don’t have anything intelligent to say further.

Conclusion

String diagrams are an intuitive and convenient representation for symmetric monoidal categories, and we’d like to do formal proofs with them in a proof assistant. But the very properties that make them so nice to use, captured naturally in the diagrammatic calculus—symmetry, associativity of the two operators, and double distributivity of each over the other—pose challenges for formal proof. In this project, I took a closer look at what those challenges are, why they arise, and what possible approaches to address them might be, including a brief survey of related work. Although I didn’t make any progress towards actually solving the problem, I understand it a lot better and I hope I will be able to share that understanding here.

Aside: I claimed at the beginning that the mathematics of string diagrams was “pretty useful”, without justification, because that was beside the point. But in case you’re curious about where they’re used, here are some directions to explore.

• Reasoning about concurrent programs [CastelloEtAl2024]

• Quantum computation [CoeckeKissinger2017] [CoeckeDuncan2011]

• Network algebra [Ştefănescu2000]

• Graphical linear algebra [Sobociński2015] and much of Sobociński’s other work

References